ANUALIDAD ANTICIPADA
Es aquella en la cual los pagos se hacen al principio de cada período. Son ejemplos de anualidades anticipadas los pagos de arrendamientos anticipados, pagos de cuotas por el financiamiento de electrodomésticos. Un ejemplo real de esta clase de anualidades se presenta en algunos créditos comerciales en los que se le manifiesta al cliente que no le cobrarán cuota inicial, pero en el mismo momento en que se hace la negociación se le exige el pago de la primera cuota del conjunto de cuotas que tiene que pagar.
El siguiente flujo de caja representa una anualidad anticipada.
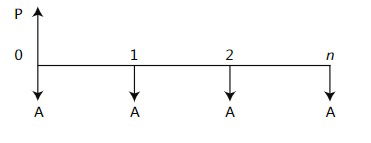
Se observa que las cuotas se pagan al principio del período. Se presenta alguna con-fusión entre las personas que se inician en el tema de las anualidades anticipadas, en lo que respecta al numero de cuotas. Por ejemplo al observar el flujo de caja se podría pensar que el valor P se esta pagando con dos cuotas, por aparecer la tercera cuota al final del período 2. En realidad, se paga con tres cuotas. En las anualidades anticipadas las cuotas se pagan al principio del periodo, y el principio del tercer periodo es el final del periodo 2.
VALOR PRESENTE DE UNA ANUALIDAD ANTICIPADA
El valor presente de una serie de pagos iguales anticipados será el valor, que en el momento de realizada la operación financiera, sea equivalente a toda la serie. En el párrafo siguiente, a través de un ejercicio, se explicarán los procedimientos más sencillos para el cálculo del valor presente de una anualidad anticipada.
EJEMPLO
Se tiene una obligación que en un momento se había pactado cancelar con 18 cuotas iguales de $ 15.000 cada una por mes anticipado. Se decide, a última hora, cancelarla de contado. Si la tasa de interés acordada es del 3% mensual, hallar este valor.
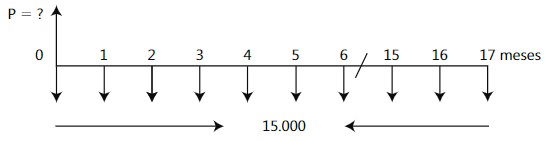
Hasta este nivel del texto, sólo conocemos las fórmulas para realizar cálculos con las anualidades vencidas. Lo recomendable, inicialmente, para trabajar con anualidades anticipadas es convertir utilizando algún artificio, la anualidad vencida. Para tal efecto, existen varios procedimientos, de los cuales se proporcionarán dos de ellos, considerados los más simples.
Procedimiento 1. Se añade, en el flujo de caja, un periodo a la izquierda.
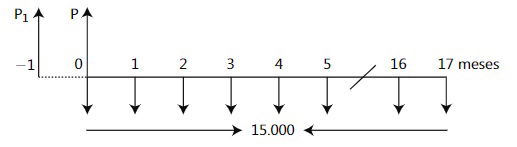
Si ignoramos P en el flujo de caja, observamos que se tiene una anualidad vencida en la que el presente es P, ubicado en -1.
Calculamos P aplicando la formula de valor presente en función de A .
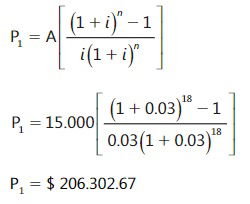
Este es el valor presente equivalente a 18 pagos mensuales de $ 15.000, a una tasa de in terés del 3% mensual, pero ubicado en el momento – 1. Como nos interesa conocer el valor presente equivalente en el momento cero, trasladamos a esta fecha el valor presente en 1. Para esto aplicamos la fórmula básica.
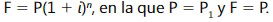
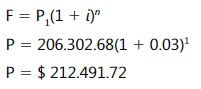
Con el procedimiento desarrollado podemos lograr una expresión que nos permita calcular el valor presente de la anualidad anticipada en una forma directa.
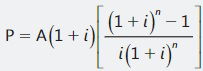
Con la fórmula desarrollada podemos plantear la siguiente regla general: el valor presente de una anualidad anticipada, ubicado en el momento en que se paga la primera cuota, resulta de multiplicar el valor presente de una anualidad vencida por (1+i)
.Reemplazando en la fórmula los valores del ejercicio, se tiene
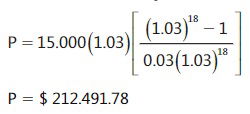
VALOR DE LA CUOTA EN UNA ANUALIDAD ANTICIPADA
Corresponde al valor de la cuota, de una serie de cuotas, que se pagan al principio del período. Para lograr una expresión que nos permita calcular su valor desarrollaremos el siguiente ejercicio, en el que aplicaremos los mismos procedimientos que utilizamos en el cálculo del valor presente.
EJEMPLO:
Se recibe un préstamo de $ 10.000.000 para pagarlo en 12 cuotas mensuales iguales, pagaderas en forma anticipada. Si le cobran el 4% de interés, calcular el valor de las cuota

Ignorando el valor P en el flujo de caja, se tiene una anualidad vencida compuesta por 12 pagos en la que el valor presente se encuentra ubicado en 1. Se calcula el valor de P1 ubicado en el momento -1, equivalente a P en el momento 0.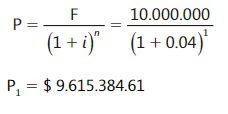
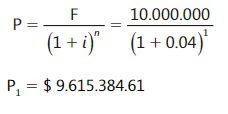
Una vez convertida la anualidad anticipada en vencida y conocidos el valor presente (P1), la tasa de interés (4%) y el número de pagos (12), podemos calcular el valor de la cuota (A), aplicando la fórmula.
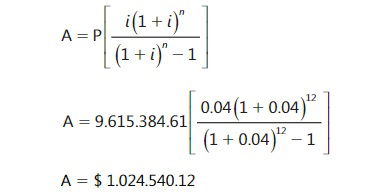 Todo este procedimiento se reduce a despejar el valor de A de la expresión
Todo este procedimiento se reduce a despejar el valor de A de la expresión 
Procedimiento 2.
Partiendo del flujo de caja inicial del prestamo, se elimina una cuota, quedando el nuevo flujo de la siguiente forma.
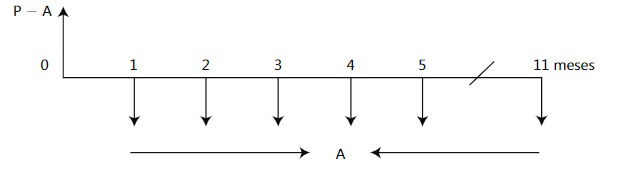
Apoyándonos en este flujo de caja podemos plantear la siguiente ecuación de valor, con fecha focal en el momento cero.
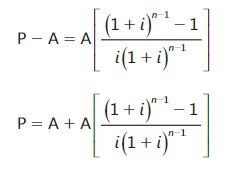
Despejando A, se tiene
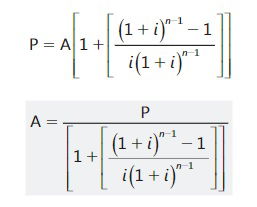
A es el valor de la cuota anticipada, P es el valor inicial de la obligación, ies la tasa de interés efectiva por período y
n es el número de cuotas.
Reemplazando los valores del ejercicio, se tiene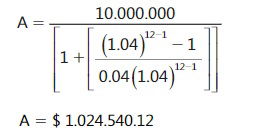
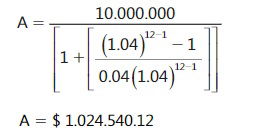
VALOR FUTURO DE UNA ANUALIDAD ANTICIPADA
Se trata ahora de calcular el valor futuro de una anualidad en la que los pagos (ingresos) se hacen al iniciarse un periodo. En el flujo de caja que se aprecia a continuación se observará que: el valor futuro de la anualidad anticipada aparece un período des-pues de realizado el último pago (ingreso), lo que indica que este pago sí devenga intereses
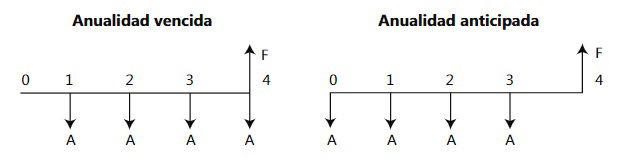
Se observa que la anualidad vencida comienza con período y termina con pago, y la anualidad anticipada comienza con pago y termina con período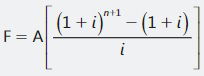 EJEMPLO:
EJEMPLO:
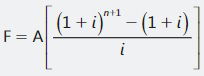 EJEMPLO:
EJEMPLO:Katya Elena recibe al principio de cada mes la suma de $ 100.000 por concepto del arriendo de una bodega de su propiedad. En el mismo momento en que recibe el pago del arriendo deposita la mitad en una cuenta de ahorros que le reconoce una tasa de interés del 3.0% mensual. Ella desea saber cuanto tendrá disponible en la cuenta a final del año. El flujo de caja se muestra a continuación.
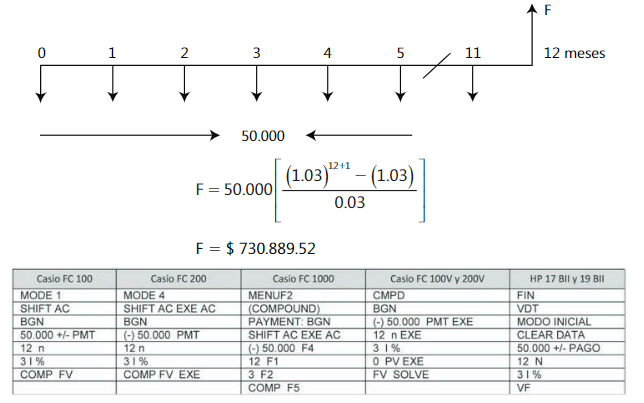
En Excel: = VF (tasa; nper; pago; VA; tipo)
= VF (3%; 12; 50.000; 0; 1)
Se ingresa el valor de 1 en el parámetro tipo, para indicar que los pagos son anticipados
Solución con la hoja de cálculo Excel
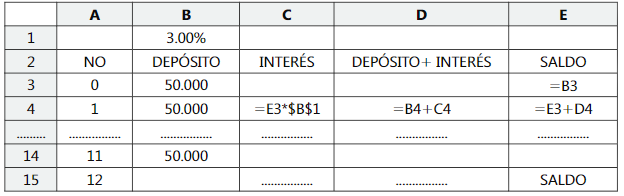
En la celda B1 escribimos la tasa de interés del 3.0%. Desde la celda B3 hasta B14 registramos el valor de los depósitos de $ 50.000. En las celdas C4, D4 y E4 calculamos intereses, deposito mas interés y saldo al final del periodo.
Rellenamos las celdas en blanco copiando las fórmulas de las celdas C4, D4 y E4 en el rango C5:E15 y encontramos un valor en E15 de $730.889.52.
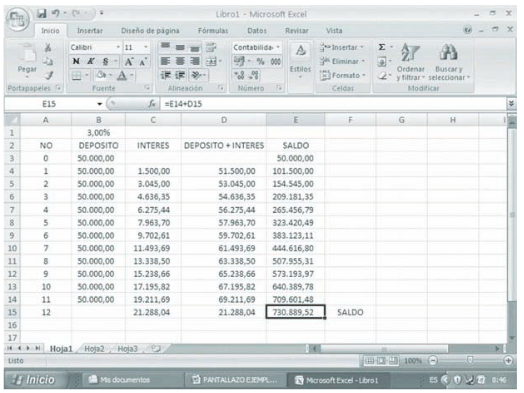
Comentarios
