ANUALIDAD PERPETUA
Es aquella en la que no existe el ultimo pago, o aquella cuyo plazo no tiene fin. Como todo en la vida tiene su final, podemos decir que una anualidad es perpetua cuando está conformada por muchos pagos, como por ejemplo, un préstamo a largo plazo en el que solamente se pagan los intereses; cuotas de mantenimiento de una carretera; el pago de un arriendo para quien nunca podrá comprar la propiedad, etc. Como la anualidad perpetua supone que los pagos son indefinidos, no existe valor futuro.
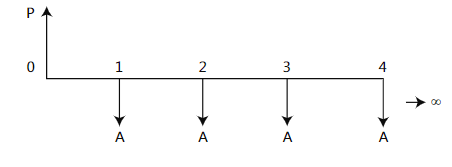
VALOR PRESENTE DE UNA ANUALIDAD PERPETUA
El valor ubicado es el presente es equivalente a una serie infinita de pagos. Su valor se calcula mediante la siguiente fórmula: 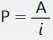
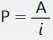
EJEMPLO:
Un inversionista decide arrendar una propiedad por $ 450.000 mensuales anticipados, en forma indefinida. Recibe una oferta que consiste en recibir un pago en el día de hoy, equivalente a toda la serie de pagos. Si su tasa de oportunidad es del 3.50% mensual, ¿ qué pago único debe aceptar? El ejercicio hace referencia a una anualidad perpetua anticipada. Para plantear la solución, nos apoyamos inicialmente en la formula que permite calcular el valor presente de una anualidad perpetua vencida. Para convertir la anualidad anticipada en vencida, utilicemos el procedimiento que consiste en eliminar la primera cuota:

El resultado indica la equivalencia entre recibir hoy un pago único de $ 13.307.142.86, a recibir en forma indefinida un arriendo de $450.000, empezando en el día de hoy.
ANUALIDAD GENERAL
En las anualidades estudiadas hasta el momento, el período de pago coincide con el período de capitalización de intereses. Todas ellas se llaman anualidades simples.
Hablamos, entonces, de pagos mensuales y conocemos la tasa de interés mensual, o pagos trimestrales y conocemos la tasa efectiva trimestral. En el caso de las anualidades generales, los períodos de pago no coinciden con los períodos de interés, por ejemplo, pagos mensuales con una tasa efectiva anual, etc.
PERÍODO DE CAPITALIZACIÓN
Es el período convenido para convertir el interés en capital. Cuando en una operación financiera se expresa una tasa del 3% mensual, esto nos indica que el periodo de capitalización es el mes.
PERÍODO DE PAGO
Es el periodo de pago o recibo de cuotas. En una operación financiera la tasa puede ser del 3% mensual, pero si las cuotas se reciben o pagan trimestralmente, el período de pago es un trimestre.
Para resolver ejercicios de anualidades generales el sistema más práctico consiste
en ajustar la tasa:
Ajustar la tasa de interés. Es decir, hacer que coincidan los períodos de interés con
los períodos de pago
EJEMPLO
El señor Pedro Picapiedra recibe un préstamo de $ 10.000.000 para pagarlo con 12 cuotas mensuales iguales. Si le cobran una tasa de interés del 38% efectivo anual, calcular el valor de las cuotas.
El siguiente es el flujo de caja:
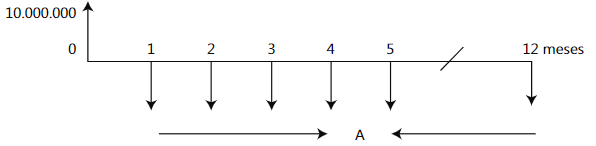
Se observa que la tasa de interés está expresada como efectiva anual y que los pagos son mensuales, por lo tanto, es necesario ajustar la tasa de interés.

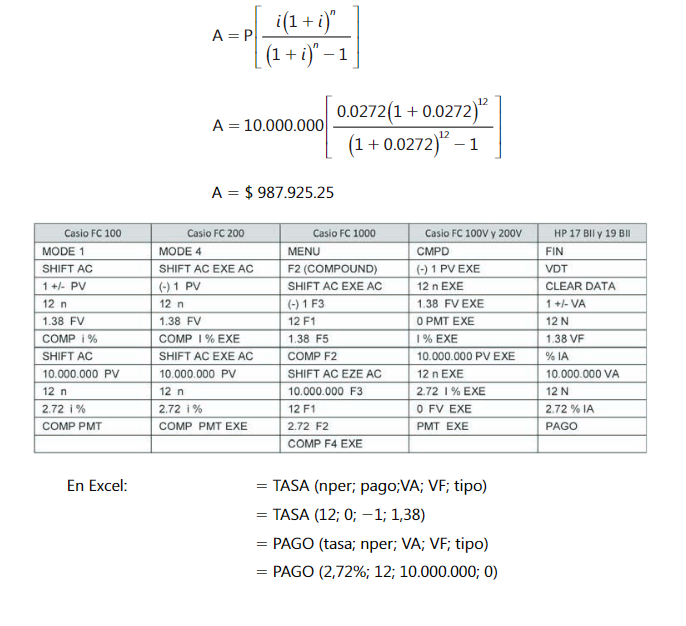
Calculamos el valor de la cuota (A) aplicando la fórmula del valor presente, conocidos: la tasa de interés, el valor presente del préstamo y el número de pagos.
Solución con Buscar objetivo de Excel
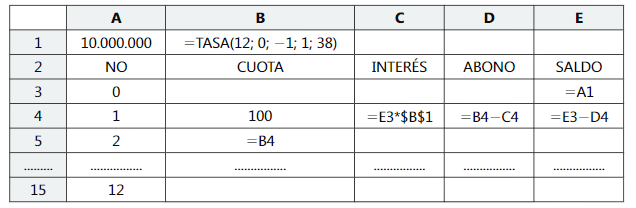
En este ejercicio la tasa de interés está expresada como efectiva anual y las cuotas de pago son mensuales, por lo tanto, se requiere convertirla en una tasa efectiva mensual equivalente, tal como aparece en la celda B1. En la celda A1 registramos el valor a financiar de $ 10.000.000. En la celda B4 escribimos 100, como valor arbitrario, y calculamos la segunda cuota en B5 y copiamos hasta B5. En las celdas C4, D4 y E4 calculamos intereses, abono a capital y saldo al final del periodo.
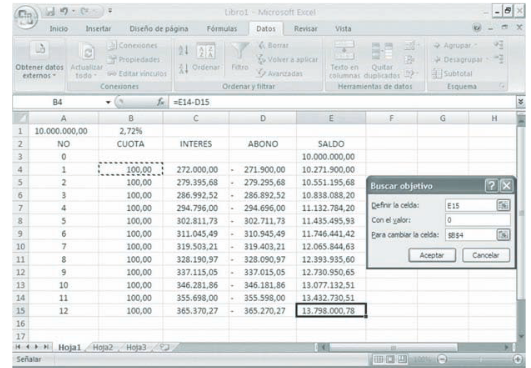
Copiamos las fórmulas de las celdas C4, D4 y E4 en el rango C5:E15 y aplicando Buscar objetivo obtenemos en B4 un valor de
$ 987.925.17, que corresponde al valor de las cuotas mensuales.
Comentarios
