ANUALIDAD VENCIDA
El flujo de caja siguiente representa una anualidad vencida donde P es el valor inicial de la obligación y A es el valor de pagos iguales y periódicos.
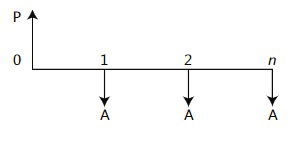
VALOR PRESENTE DE UNA ANUALIDAD VENCIDA
Es un valor, ubicado un período anterior a la fecha del primer pago, equivalente a una serie de pagos iguales y periódicos. Desde el punto de vista matemático, es la suma de los valores presentes de todos los pagos.
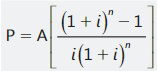
se calcula un valor presente equivalente (P) a una serie de pagos iguales y periódicos, conocidos el número de pagos (n), el valor de cada pago (A) y la tasa de interés (i). En otros términos, reemplaza una serie de pagos iguales llamada anualidad, por un valor presente equivalente P. El error más frecuente que se comete al trabajar problemas de anualidades es la colocación incorrecta de P, razón por la cual, es importante recordar la siguiente regla: el valor presente (P) estará ubicado al principio del período en que se hace el primer pago (A). Para el caso de flujo utilizado, y cuando el primer pago se hace en 1, valor presente quedará ubicado en el momento cero. ¿Por qué? porque se dedujo con P en el momento cero y A al final del primer periodo.
EJEMPLO
Se compró un vehículo con una cuota inicial de $ 1.000.000 y 12 cuotas mensuales
iguales de $ 200.000. La agencia cobra el 2.5% mensual sobre saldos. Calcular el valor
del vehículo.
Cuota inicial $ 1.000.000
A =$ 200.000 n =12 i = 2.5% mensual P = ?
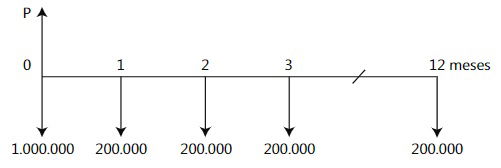
Tal como se mencionó en el ejemplo (5.1), la solución primaria a este problema se logra planteando una ecuación de valor con fecha focal en el momento cero, de la siguiente forma: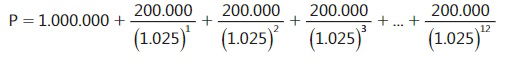
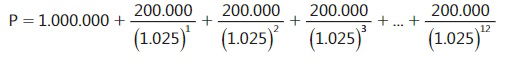
Este procedimiento resulta tedioso porque implica trasladar en forma individual 12 valores del futuro al presente. Aplicando la fórmula (5.1) se calcula el valor presente de las 12 cuotas iguales, que quedará ubicado al principio del período en el que se hace el primer pago.
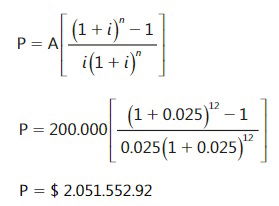
El valor del vehículo será igual al valor presente de los 12 pagos iguales más la cuota inicial.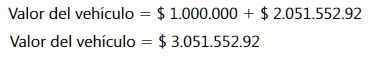
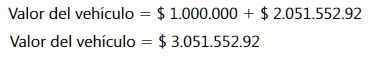
Es equivalente pagar en el día de hoy la suma de $ 3.051.552.92, que cancelar hoy una cuota inicial de $ 1.000.000 y 12 cuotas mensuales iguales de $ 200.000, si la tasa de interés es del 2.5% mensual.
VALOR PRESENTE DE UNA ANUALIDAD VENCIDA CON TASA VARIABLE
En los ejemplos 5.2 y 5.3 hemos calculado el valor presente de un conjunto de valores periódicos y de igual monto (Anualidad) bajo el supuesto de que la tasa de interés para cada período permanece constante, que es lo que supone el factor (1+i)n de la fórmula del valor presente de una anualidad vencida. En muchas ocasiones se deben calcular valores presentes de cuotas uniformes con tasas variables y en estos casos no aplica la fórmula, de tal forma que debemos diseñar un procedimiento con la hoja de cálculo Excel para poder encontrar una solución.
EJEMPLO
Calcular el valor presente de 4 cuotas mensuales de $ 200 dadas las siguientes tasas de interés.
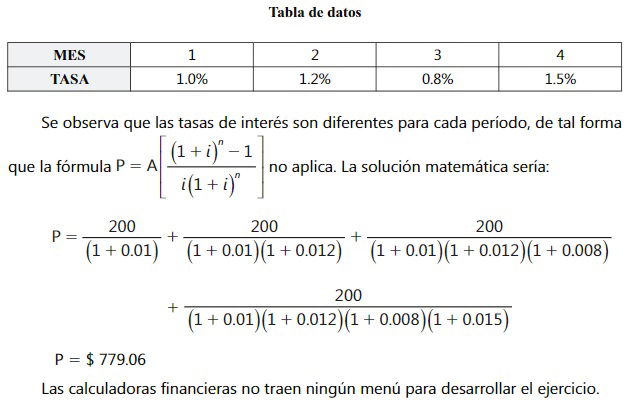 Solución con la hoja de cálculo Excel
Solución con la hoja de cálculo Excel
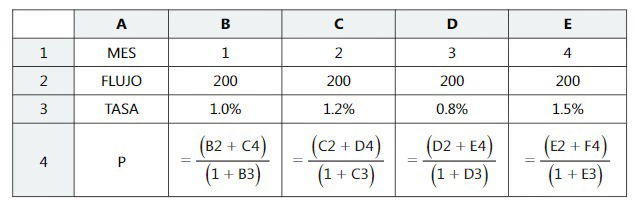
Para calcular el valor presente se hace necesario construir una fórmula, de los períodos más lejanos hasta los más cercanos, en cuyo numerador se sume lo que viene del periodo posterior (F4) con flujo del mes (E2), y en el denominador se descuente la tasa del período. Esta fórmula se copia para los períodos anteriores, lográndose el efecto acumulativo, de tal forma que en la celda B4 obtenemos el valor presente equivalente. (Ver tabla de datos y hoja de cálculo en excel de este ejemplo)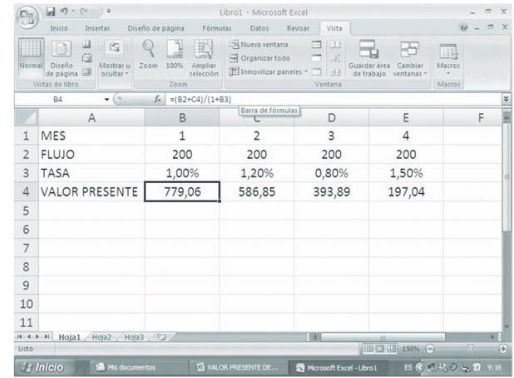

.
VALOR DE LA CUOTA EN FUNCIÓN DEL VALOR PRESENTE
Conocidos el valor presente (P), la tasa de interés (i) y el número de pagos (n), podemos calcular el valor de la cuota. Si de la fórmula del valor presente (5.1) despejamos el valor de la cuota A, tenemos:
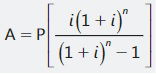
El valor entre llaves se denomina
factor de recuperación de capital.
EJEMPLO
Un lote de terreno que cuesta $ 20.000.000 se propone comprar con una cuota inicial del 10% y 12 cuotas mensuales con una tasa de interés del 2% mensual. Calcular el valor de las cuotas.
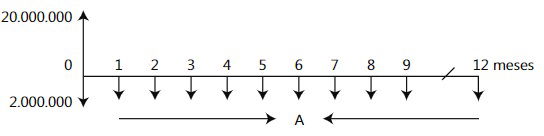
Al restarle al valor del terreno la cuota inicial de $ 2.000.000 queda el saldo de la deuda que se va a financiar por medio de 12 cuotas mensuales.
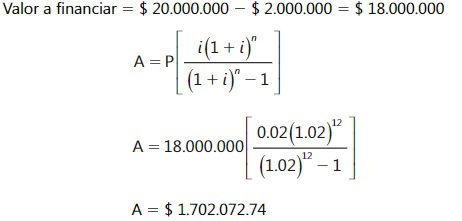
Cada mes, durante 12 meses, se deben pagar $ 1.702.072.74 para cancelar el saldo de la deuda de $ 18.000.000
VALOR FUTURO DE UNA ANUALIDAD VENCIDA
Es un valor ubicado en la fecha del último pago, equivalente a toda la serie de pagos iguales y periódicos. En forma matemática, es el valor final que resulta de sumar todos los valores llevados al futuro. El flujo que analizaremos a continuación tiene tres pasos iguales de A, y se desea calcular su valor futuro equivalente ubicado en la fecha del último pago.
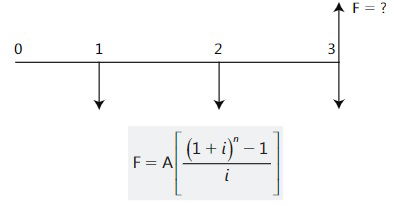
Por medio de la fórmula se calcula el valor futuro equivalente a una serie de pagos iguales, conocidos el valor de cada pago (A), la tasa de interés (i) y el número de pagos o ingresos (n). Por la forma como se dedujo, el valor futuro equivalente a una serie de pagos iguales vencidos queda ubicado en la fecha en que se hace el último pago.
VALOR DE LA CUOTA EN FUNCIÓN DEL VALOR FUTURO
Conocidos el valor futuro equivalente a una serie de pagos iguales (F), la tasa de interés efectiva periódica (i) y el número de pagos (n), se desea calcular el valor de la cuota igual y periódica. De la fórmula (5.3) despejamos el valor de A y se obtiene:
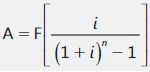
EJEMPLO
¿Cuanto se debe depositar al final de cada mes, durante dos años, en una cuenta de ahorros que reconoce una tasa del 2.50% mensual para reunir la suma de $ 8.500.000?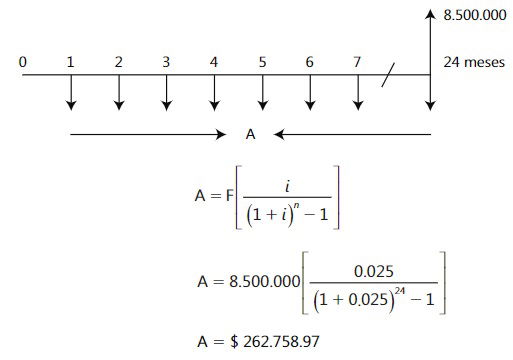

Comentarios
